Happy studying! Did you find my notes useful this semester? Please consider giving me a few bucks or buying me a beer. Contributions like yours help me keep these notes forever free.
Start Here
Lecture Notes
Generating Uniform Random Numbers
- Introduction
- Some Lousy Generators
- Random Devices
- Random Number Tables
- Mid-Square Method
- Fibonacci and Additive Congruential Generators
- Linear Congruential Generator
- LCGs
- Trivial Example
- Easy Exercise
- Better Example
- What Can Go Wrong?
- RANDU Generator
- Exercises
- Tausworthe Generators
- Tausworthe Generator
- Example
- Generating Uniforms
- Generalizations of LCGs
- A Simple Generalization
- Combinations of Generators
- A Really Good Combined Generator
- Some Remarks
- Choosing a Good Generator - Theory
- Theorem
- Theorem
- Theorem
- Geometric Considerations
- One-Step Serial Correlation
- Choosing a Good Generator - Stats Test
- Statistical Tests Intro
- Choosing a Good Generator - Goodness-of-Fit Tests
- Chi-Squared Goodness-of-Fit Test
- Illustrative Example
- Choosing a Good Generator - Independence Tests I
- Independence - Runs Tests
- Runs Test "Up and Down"
- Up and Down Example
- Runs Test "Above and Below the Mean"
- Above and Below the Mean Example
- Choosing a Good Generator - Independence Tests II (OPTIONAL)
- Correlation Test
- Example
Happy studying! Did you find my notes useful this semester? Please consider giving me a few bucks or buying me a beer. Contributions like yours help me keep these notes forever free.
Start Here
Lecture Notes
Generating Uniform Random Numbers
- Introduction
- Some Lousy Generators
- Random Devices
- Random Number Tables
- Mid-Square Method
- Fibonacci and Additive Congruential Generators
- Linear Congruential Generator
- LCGs
- Trivial Example
- Easy Exercise
- Better Example
- What Can Go Wrong?
- RANDU Generator
- Exercises
- Tausworthe Generators
- Tausworthe Generator
- Example
- Generating Uniforms
- Generalizations of LCGs
- A Simple Generalization
- Combinations of Generators
- A Really Good Combined Generator
- Some Remarks
- Choosing a Good Generator - Theory
- Theorem
- Theorem
- Theorem
- Geometric Considerations
- One-Step Serial Correlation
- Choosing a Good Generator - Stats Test
- Statistical Tests Intro
- Choosing a Good Generator - Goodness-of-Fit Tests
- Chi-Squared Goodness-of-Fit Test
- Illustrative Example
- Choosing a Good Generator - Independence Tests I
- Independence - Runs Tests
- Runs Test "Up and Down"
- Up and Down Example
- Runs Test "Above and Below the Mean"
- Above and Below the Mean Example
- Choosing a Good Generator - Independence Tests II (OPTIONAL)
- Correlation Test
- Example
Simulation
Generating Uniform Random Numbers
44 minute read
Notice a tyop typo? Please submit an issue or open a PR.
Generating Uniform Random Numbers
Introduction
Uniform(0,1) random numbers are the key to all random variate generation and simulation. As we have discussed previously, we transform uniforms to get other random variables - exponential, normal, and so on.
The goal is to produce an algorithm that can generate a sequence of pseudo-random numbers (PRNs) R1,R2,... that "appear" to be i.i.d Uniform(0,1). Of course, these numbers are not truly uniform because they are neither independent of one another, nor are they random. However, they will appear random to humans, and they will have all the statistical properties of i.i.d Uniform(0,1) random numbers, so we are allowed to use them.
Such an algorithm has a few desired properties. As we said, we need to produce output that appears to be i.i.d Unif(0,1). We also need the algorithm to execute quickly because we might want to generate billions of PRNs. Moreover, we need the algorithm to be able to reproduce any sequence it generates. This property allows us to replicate experiments and simulation runs that rely on streams of random numbers.
In the next few lessons, we will look at different classes of Unif(0,1) generators. We'll start with some lousy generators, such as
- the output of a random device
- a table of random numbers
- the mid-square method
- the Fibonacci method
We will then move on to the more common methods used in practice: the linear congruential generators and the Tausworthe generator. Finally, we'll talk about hybrid models, which most people use today.
Some Lousy Generators
In this lesson, we will spend some time talking about poor generators. Obviously, we won't use these generators in practice, but we can study them briefly both for a historical perspective and to understand why they are so bad.
Random Devices
We'll start our discussion by looking at random devices. A coin toss is a random device that can help us generate values of zero or one randomly. Similarly, we can roll a die to generate a random number between one and six. More sophisticated random devices include Geiger counters and atomic clocks.
Naturally, random devices have strong randomness properties; however, we cannot reproduce their results easily. For example, suppose we ran an experiment based off of one billion die rolls. We'd have to store the results of those rolls somewhere if we ever wanted to replicate the experiment. This storage requirement makes random devices unwieldy in practice.
Random Number Tables
We can also use random number tables. These tables are relatively ubiquitous, although they have fallen out of use since the 1950s. This table, published by the RAND corporation, contains one million random digits and one hundred thousand normal random variates. Basically, folks used a random device to generate random numbers, and then they wrote them down in a book.
How do we use this book? Well, we can simply flip to a random page, put our finger down in the middle of the page, and start reading off the digits.
While this approach has strong reproducibility and randomness properties, it hasn't scaled to meet today's needs. More specifically, a finite sequence of one million random numbers is just not sufficient for most applications. We can consume a billion random numbers in seconds on modern hardware. Additionally, once the digits were tabled, they were no longer random.
Mid-Square Method
The mid-square method was created by the famous mathematician John von Neumann. The main idea here is we take an integer, square it, and then use the middle part of that integer as our next random integer, repeating the process as many times as we need. To generate the Uniform(0,1) random variable, we would divide each generated integer by the appropriate power of ten.
Let's look at an example. Suppose we have the seed X0=6632. If we square X0, we get 66322=43983424, and we set X1 equal to the middle four digits: X1=9834. We can generate X2 in a similar fashion: X12=98342=96707556, so X2=7075. Now, since we are taking the middle four integers, we generate the corresponding Uniform(0,1) random variate, Ri, by dividing Xi by 10000. For example, R1=X1/10000=9834/10000=0.9834, and R2=0.7075 by similar arithmetic.
Unfortunately, it turns out that there is a positive serial correlation in the Ri's. For example, a very small Xi+1 often follows a very small Xi, more so than we would expect by random chance. More tragically, the sequence occasionally degenerates. For example, if Xi=0003, then the sequence ends up producing only zeros after a certain point.
Fibonacci and Additive Congruential Generators
The Fibonacci and additive congruential generators, not to be confused with the linear congruential generators, are also no good.
Here is the expression for the Fibonacci generator, which got its name got its name from the famed sequence that involves adding the previous two numbers to get the current number.
For this sequence, X−1 and X0 are seeds, and m is the modulus. Remember that a=bmodm if and only if a is the remainder of b/m. For example, 6=13mod7.
Like the mid-square method, this generator has a problem where small numbers frequently follow small numbers. Worse, it turns out the one-third of the values for each subsequent uniform are impossible to calculate. Particularly, it is impossible to compute an Xi+1, such that Xi−1<Xi+1<Xi, or Xi<Xi+1<Xi−1. Those two configurations should occur one-third of the time, which means that this generator does not have strong randomness properties.
Linear Congruential Generator
In this lesson, we will ditch the lousy pseudo-random number generators and turn to a much better alternative: the linear congruential generator (LCG). Variations of LCGs are the most commonly used generators today in practice.
LCGs
Here is the general form for an LCG. Given a modulus, m, and the constants a and c, we generate a pseudo-random integer, Xi, and its corresponding Uniform(0,1) counterpart, Ri, using the following equations:
We choose a, c, and m carefully to ensure both that the Ri's appear to be i.i.d uniforms and that the generator has long periods or cycle lengths: the amount of time until the LCG starts to repeat.
Multiplicative generators are LCGs where c=0.
Trivial Example
Let's look at an example. Consider the following LCG:
Starting with the seed, X0=0, we can generate the following sequence of values:
Notice that this sequence starts repeating with after eight observations: X8=X0=0. This generator is a full-period generator since it has a cycle length equal to m. Generally speaking, we prefer full-period generators, but we would never use this particular generator in practice because the modulus is much too small.
Let's consider the following plot of all (Xi−1,Xi) coordinate pairs. For example, the point (0,3) corresponds to (X0,X1). Notice that we also include the point (−2,1). We can observe that −2mod8=6mod8=6.
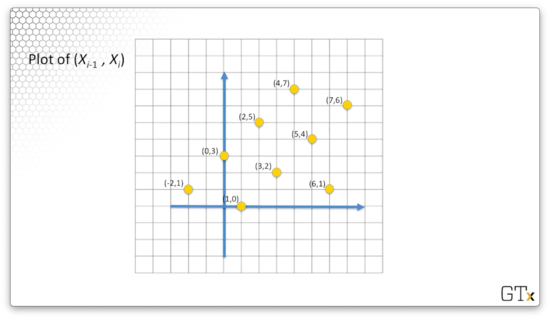
What's interesting about this plot is that the pseudo-random numbers appear to fall on lines. This feature is a general property of the linear congruential generators.
Easy Exercise
Consider the following generator:
Does this generator achieve full cycle? Let's find out:
If we seed this sequence with an odd number, we only see odd numbers. Similarly, if we seed this sequence with an even number, we only see even numbers. Regardless, this sequence repeats after four observations, and, since the modulus is eight, this generator does not achieve full cycle.
Better Example
Let's look at a much better generator, which we have seen before:
This particular generator has a full-period (greater than two billion) cycle length, except when X0=0.
Let's look at the algorithm for generating each Xi and Ri:
As an example, if X0=12345678, then:
What Can Go Wrong?
As we saw, we can have generators like Xi=(5Xi−1+2)mod8, which only produce even integers and are therefore not full-period. Alternatively, the generator Xi=(Xi−1+1)mod8 is full-period, but it produces very non-random output: X1=1, X2=2, and so on.
In any case, if the modulus m is "small", we'll get unusably short cycling whether or not the generator is full period. By small, we mean anything less than two billion or so. However, just because m is big, we still have to be careful because subtle problems can arise.
RANDU Generator
Let's take a look at the RANDU generator, which was popular during the 1960s:
Unfortunately, the numbers that this LCG generates are provably not i.i.d., even from a statistical point of view.
Let's take a sufficiently large i and plot the points (Ri−2,Ri−1,Ri) within a unit cube. If the numbers generated from this sequence were truly random, we would see a random dispersion of dots within the cube. However, the random numbers fall entirely on fifteen hyperplanes.

Exercises

Tausworthe Generators
In this lesson, we will look at the Tausworthe generator.
Tausworthe Generator
Let's take a look at the Tausworthe generator. We will define a sequence of binary digits, B1,B2,..., as:
In other words, we calculate each Bi by taking the sum of the q previous cjBi−j products, where cj∈{0,1}. We take the entire sum mod2, so every Bi is either a one or a zero.
Instead of using the previous q entries in the sequence to compute Bi, we can use a shortcut that saves a lot of computational effort, which takes the same amount of time regardless of the size of q:
Remember that any Bi can only be either 0 or 1. Consider the following table:
Now, let's consider the XOR operator. If we think of the OR operator as, colloquially, "either this or that", we can think of the XOR as "either this or that, but not both"; indeed, XOR is an abbreviation of "eXclusive OR". Let's look at the truth table:
Thus, we can see that (Bi−r+Bi−q)mod2 and Bi−r XOR Bi−q are indeed equivalent. Of course, we might use an even simpler expression to compute Bi, which doesn't involve XOR:
To initialize the Bi sequence, we need to specify, B1,B2,...,Bq.
Example
Let's look at an example. Consider r=3,q=5;B1=⋯=B5=1. Thus, for i>5, Bi=Bi−3 XOR Bi−5. For example, B6=B3 XOR B1=0 and B7=B4 XOR B2=0. Let's look at the first 36 values in the sequence:
Generally, the period of these bit sequences is 2q−1. In our case, q=5, so 25−1=31. Indeed, the thirty-second bit restarts the sequence of five ones that we see starting from the first bit.
Generating Uniforms
How do we get Unif(0,1) random variables from the Bi's? We can take a sequence of l bits and divide them by 2l to compute a real number between zero and one.
For example, suppose l=4. Given the sequence of bits in the previous sequence, we get the following sequence of randoms:
Tausworthe generators have a lot of potential. They have many nice properties, including long periods and fast calculations. Like with the LCGs, we have to make sure to choose our parameters - q, r, B1,⋯,Bq, and l - with care.
Generalizations of LCGs
In this lesson, we will return to the LCGs and look at several generalizations, some of which have remarkable properties.
A Simple Generalization
Let's consider the following generalization:
Generators of this form can have extremely large periods - up to mq−1 if we choose the parameters correctly. However, we need to be careful. The Fibonacci generator, which we saw earlier, is a special case of this generalization, and it's a terrible generator, as we demonstrated previously.
Combinations of Generators
We can combine two generators, X1,X2,... and Y1,Y2,..., to construct a third generator, Z1,Z2,.... We might use one of the following techniques to construct the Zi's:
- Set Zi equal to (Xi+Yi)modm
- Shuffling the Xi's and Yi's
- Set Zi conditionally equal to Xi or Yi
However, the properties for these composite generators are challenging to prove, and we should not use these simple tricks to combine generators.
A Really Good Combined Generator
The following is a very strong combined generator. First, we initialize X1,0,X1,1,X1,2,X2,0,X2,1,X2,2. Next, for i≥3:
As crazy as this generator looks, it only requires simple mathematical operations. It works well, it's easy to implement, and it has an amazing cycle length of about 2191.
Some Remarks
Matsumoto and Nishimura have developed the "Mersenne Twister" generator, which has a period of 219937−1. This period is beyond sufficient for any modern application; we will often need several billion PRNs, but never more than even 2100. All standard packages - Excel, Python, Arena, etc. - use one of these "good" generators.
Choosing a Good Generator - Theory
In this lesson, we will discuss some PRN generator properties from a theoretical perspective, and we'll look at an amalgamation of typical results to aid our discussion.
Theorem
Suppose we have the following multiplicative generator:
This generator can have a cycle length of at most 2n−2, which means that this generator is not full-cycle. To make matters worse, we can only achieve this maximum cycle length when X0 is odd and a=8k+3 or a=8k+5, for some k.
For example, suppose Xi=13Xi−1mod64. Note that a=8k+5,k=1 and n=26=64. Consider the following sequence of values:
We can see that we have cycled after 2n−2=24=16 entries. What happens to the cycle length if X0 is even?
Here, we cycle after 2n−3=8 entries. Let's look at the cycle for X0=3. As we can see, our cycle length increases back to 2n−2:
Finally, let's look at the sequence when X0=4. As we can see, when we seed the generator with this value, our cycle length drops to four.
Theorem
Suppose we have the following linear congruential generator:
This generator has full cycle if the following three conditions hold:
- c and m are relatively prime
- a−1 is a multiple of every prime which divides m
- a−1 is a multiple of 4 if 4 divides m
Let's look at a corollary to this theorem. Consider the following special case of the general LCG above:
This generator has full cycle if c is odd and a=4k+1 for some k.
Theorem
Suppose we have the following multiplicative generator:
This generator has full period (m−1, in this case), if and only if the following two conditions hold:
- m divides am−1−1
- for all integers i<m−1, m does not divide ai−1
We define the full period as m−1 in this case because, if we start at X0=0, we just cycle at zero.
For m=231−1, it can be shown that 534,600,000 multipliers yield full period. In some sense, a=950,706,376 is the "best" multiplier, according to this paper by Fishman and Moore from 1986.
Geometric Considerations
Let's look at k consecutive PRNs, (Ri,...,Ri+k−1),i≥1, generated from a multiplicative generator. As it turns out, these k-tuples lie on parallel hyperplanes in a k-dimensional unit cube.
We might be interested in the following geometric optimizations:
- maximizing the minimum number of hyperplanes in all directions
- minimizing the maximum distance between parallel hyperplanes
- maximizing the minimum Euclidean distance between adjacent k-tuples
Remember that the RANDU generator is particularly bad because the PRNs it generates only lie on 15 hyperplanes.
One-Step Serial Correlation
We can also look at a property called one-step serial correlation, which measures how adjacent are correlated with each other. Here's a result from this paper by Greenberg from 1961:
Remember that a is the multiplicative constant, c is the additive constant, and m is the modulus.
This upper bound is very small when m is in the range of two billion, and a is, say, 16807. This result is good because it demonstrates that small Xi's don't necessarily follow small Xi−1's, and large Xi's don't necessarily follow large Xi−1's.
Choosing a Good Generator - Stats Test
In this lesson, we'll give an overview of various statistical tests for goodness-of-fit and independence. We'll conduct specific tests in subsequent lessons.
Statistical Tests Intro
We will look at two general classes of tests because we have a couple of goals we want to accomplish when examining how well pseudo-random number generators perform.
We run goodness-of-fit tests to ensure that the PRNs are approximately Unif(0,1). Generally speaking, we will look at the chi-squared test to measure goodness-of-fit, though there are other tests available. We also run independence tests to determine whether the PRNs are approximately independent. If a generator passes both tests, we can assume that it generates approximately i.i.d Unif(0,1) random variables.
All the tests that we will look at are hypothesis tests: we will test our null hypothesis (H0) against an alternative hypothesis (H1).
We regard H0 as the status quo - "that which we currently believe to be true". In this case, H0 refers to the belief that the numbers we are currently generating are, in fact, i.i.d Unif(0,1).
If we get substantial, observational evidence that H0 is wrong, then we will reject it in favor of H1. In other words, we are innocent until proven guilty, at least from a statistical point of view.
When we design a hypothesis test, we need to set the level of significance, α, which is the probability that we reject H0, given it is true: α=P(Reject H0∣H0 true). Typically, we set α equal to 0.05 or 0.1. Rejecting a true H0 is known as a Type I Error.
Selecting a value for α informs us of the number of observations we need to take to achieve the conditional probability to which α refers. For example, if we set α to a very small number, we typically have to draw more observations than if we were more flexible with α.
We can also specify the probability of a Type II Error, which is the probability, β, of accepting H0, given that it is false: β=P(Accept H0∣H0 false). We won't focus on β much in these lessons.
Usually, we are much more concerned with avoiding incorrect rejections of H0, so α tends to be the more important of the two measures.
For instance, suppose we have a new anti-cancer drug, and it's competing against our current anti-cancer drug, which has average performance. Our null hypothesis would likely be that the current drug is better than the new drug because we want to keep the status quo. It's a big problem if we reject this hypothesis and replace it with a less effective drug; indeed, it's a much worse situation than not replacing it with a superior drug.
Choosing a Good Generator - Goodness-of-Fit Tests
In this lesson, we'll look at the chi-squared goodness-of-fit test to check whether or not the PRNs we generate are indeed Unif(0,1). There are many goodness-of-fit tests in the wild, such as the Kolmogorov-Smirnov test and the Anderson-Darling test, but chi-squared is the most tried-and-true. We'll look at how to do goodness-of-fit tests for other distributions later.
Chi-Squared Goodness-of-Fit Test
The first thing we need to consider when designing this test is what our null hypothesis ought to be. In this case, we assume that our PRNs are Unif(0,1). Formally, H0: R1,R2,...,Rn∼Unif(0,1). As with all hypothesis tests, we assume that H0 is true until we have ample evidence to the contrary, at which point we reject H0.
To start, let's divide the unit interval, [0,1], into k adjacent sub-intervals of equal width: [0,1/k),[1/k,2/k),...,[(k−1)/k,1]. If our alleged uniforms are truly uniform, then the probability that any one observation Rj will fall in a particular sub-interval is 1/k.
Next, we'll draw n observations, R1,...,Rn, and observe how many fall into each of the k cells. Let Oi equal the number of Rj's that fall in sub-interval i. Given n trials, and a probability of 1/k of landing in sub-interval i, we see that each Oi is distributed as a binomial random variable: Oi∼Bin(n,1/k),i=1,2,...,k. Note that we can only describe Oi in this way if we assume that the Rj's are i.i.d.
Since Oi is a binomial random variable, we can define the expected number of Rj's that will fall in cell i as: Ei=E[Oi]=n/k,i=1,2,...,k. Remember that, by definition, the expected value of a Bin(n,p) random variable is np.
We reject the null hypothesis that the PRNs are uniform if the Oi's don't match the Ei's well. In other words, if our observations don't match our expectations, under the assumption that H0 is true, then something is wrong. The only thing that could be wrong is the null hypothesis.
The goodness-of-fit statistic, χ2, gives us some insight into how well our observations match our expectations. Here's how we compute χ2:
Note the subscript of 0. All this means is that χ02 is a statistic that we collect by observation.
In layman's terms, we take the sum of the squared differences of each of our observations and expectations, and we standardize each squared difference by the expectation. Note that we square the difference so that negative and positive deviations don't cancel.
If the observations don't match the expectations, then χ02 will be a large number, which indicates a bad fit. When we talk about "bad fit" here, what we are saying is that describing the sequence of PRNs as being approximately Unif(0,1) is inappropriate: the claim doesn't fit the data.
As we said, Oi is a binomial random variable. For large values of n and k, binomial random variables are approximately normal. If Ei is the expected value of Oi, then (Oi−Ei)∼Nor(0,σ2).
As it turns out, the quantity (Oi−Ei)2 is a χ2 random variable, and, by dividing it by Ei, we standardize it to a χ2 random variable with one degree of freedom. If we add up k χ2 random variables, we get a χ2 random variable with k degrees of freedom.
Note that the Oi's are correlated with one another; in other words, if Rj falls in one sub-interval, it cannot fall in another sub-interval. The number of observations that land in one sub-interval is obviously dependent on the number that land in the other sub-intervals.
All this to say: we don't actually get k degrees of freedom, in our resulting χ2 random variable, we only get k−1. We have to pay a penalty of one degree of freedom for the correlation. In summary, by the central limit theorem, χ02∼χk−12, if H0 is true.
Now, we can look up various (1−a) quantiles for χ2 distributions with varying degrees of freedom, n, where we define a quantile, χα,n2 as: P(χn2<χα,n2)=1−α. In our case, we reject the null hypothesis if our test statistic, χ02, is larger than χα,k−12, and we fail to reject H0 if χ02≤χα,k−12.
The usual recommendation from an introductory statistics class for the χ2 goodness-of-fit test is to pick large values for k and n: Ei=n/k should be at least five, and n should be at least 30.
However, when we test PRN generators, we usually have massive values for both n and k. When k is so large we can't find tables with values for χa,k−12, we can approximate the χ2 quantile using the following expression:
Note that za is the appropriate standard normal quantile.
Illustrative Example
Suppose we draw n=1000 observations, and we've divided the unit interval into k=5 equal sub-intervals. The expected number of observations that fall into each interval is Ei=n/k=200. Let's look at the observations we gathered:
Let's compute the goodness-of-fit statistic:
Since k=5, we are looking at a χ2 distribution with four degrees of freedom. Let's choose α=0.05. Now, we need to look up the χ0.05,42 quantile in a table, which has a value of 9.49. Since our test statistic is less than the quantile, we fail to reject H0. We can assume that these observations are approximately uniform.
Choosing a Good Generator - Independence Tests I
In this lesson, we'll look at the so-called "runs" tests for independence of PRNs. There are many other tests - correlation tests, gap test, poker tests, birthday tests, etc. - but we'll focus specifically on two types of runs tests.
Interestingly, we find ourselves in something of a catch-22: the independence tests all assume that the PRNs are Unif(0,1), while the goodness-of-fit tests all assume that the PRNs are independent.
Independence - Runs Tests
Let's consider three different sequences of coin tosses:
In example A, we have a high negative correlation between the coin tosses since tails always follows heads and vice versa. In example B, we have a high positive correlation, since similar outcomes tend to follow one another. We can't see a discernible pattern among the coin tosses in example C, so observations might be independent in this sequence.
A run is a series of similar observations. In example A above, there are ten runs: "H", "T", "H", "T", "H", "T", "H", "T", "H", "T". In example B, there are two runs: "HHHHH", "TTTTT". Finally, in example C, there are six runs: "HHH", "TT", "H", "TT", "H", "T".
In independence testing, our null hypothesis is that the PRNs R1,R2,...,Rn are independent. A runs test rejects the null hypothesis if there are "too many" or "too few" runs, provided we quantify the terms "too many" and "too few". There are several types of runs tests, and we'll look at two of them.
Runs Test "Up and Down"
Consider the following PRNs:
In the "up and down" runs test, we look to see whether we go "up" or "down" as we move from PRN to PRN. Going from .41 to .68, we go up. Going from .68 to 0.89, we go up. Going from 0.89 to 0.84, we go down. From 0.84 to 0.74, we go down again.
Let's transform our sequence of PRNs into one of plusses and minuses, where a plus sign indicates going up, and a minus sign indicates going down:
Here are the associated runs - there are six in total - demarcated by commas:
Let A denote the total number of up and down runs out of the n observations. Like we said, A=6 in this example. If n is large (say, ≥20), and the Rj's are indeed independent, then A is approximately normal, with the following parameters:
Let's transform A into a standard normal random variable, Z0, which we accomplish with the following manipulation:
Now we can finally quantify "too large" and "too small". Specifically, we reject H0 if the absolute value of Z0 is greater than the α/2 standard normal quantile:
Up and Down Example
Suppose we have observed A=55 runs over n=100 observations. Given these variables, A is approximately normal with the following parameters:
Let's compute Z0:
If α=0.05, then zα/2=1.96 and we reject H0, thereby rejecting independence.
Runs Test "Above and Below the Mean"
Let's look at the same sequence of PRNs:
Let's transform our sequence of PRNs into one of plusses and minuses, where a plus sign indicates that Ri≥0.5, and a minus sign indicates that Ri<0.5:
Here are the associated runs - there are three in total - demarcated by commas:
If n is large (say, ≥20), and the Rj's are indeed independent, then the number of runs, B, is again approximately normal, with the following parameters:
Note that n1 refers to the number of observations greater than or equal to the mean and n2=n−n1.
Let's transform B into a standard normal random variable, Z0, which we accomplish with the following manipulation:
Again, we reject H0 if the absolute value of Z0 is greater than the α/2 standard normal quantile:
Above and Below the Mean Example
Consider the following +/− sequence of n=40 observations:
In this case, we have n1=18 observations above the mean and n2=22 observations below the mean, as well as B=17 runs. Without walking through the algebra, we can compute that B≈Nor(20.3,9.54).
Let's compute Z0:
If α=0.05, then zα/2=1.96, and we fail to reject H0. Therefore, we can treat the observations in this sequence as being independent.
Choosing a Good Generator - Independence Tests II (OPTIONAL)
In this lesson, we'll look at another class of tests, autocorrelation tests, that we can use to evaluate whether pseudo-random numbers are independent.
Correlation Test
Given a sequence of PRNs, R1,R2,...Rn, and assuming that each Ri is Unif(0,1), we can conduct a correlation test against the null hypothesis that the Ri's are indeed independent.
We define the lag-1 correlation of the Ri's by ρ≡Corr(Ri,Ri+1). In other words, the lag-1 correlation measures the correlation between one PRN and its immediate successor. Ideally, if the PRNs are uncorrelated, ρ should be zero.
A good estimator for ρ is given by:
In particular, if n is large, and H0 is true:
Let's transform ρ^ into a standard normal random variable, Z0, which we accomplish with the following manipulation:
We reject H0 if the absolute value of Z0 is greater than the α/2 standard normal quantile:
Example
Consider the following n=30 PRNs:
After some algebra, we get ρ^=0.950 and Var(ρ^)=0.441. Notice how high our correlation estimator is; we might expect a robust rejection of the null hypothesis.
Let's compute Z0:
If α=0.05, then zα/2=1.96, and we fail to reject H0. Therefore, we can treat the observations in this sequence as being independent. In this case, n=30 observations is quite small, and we might indeed reject H0, given such a high correlation, if we were to collect more observations.
OMSCS Notes is made with in NYC by Matt Schlenker.
Copyright © 2019-2023. All rights reserved.
privacy policy