Secure Computer Systems
Database Security Basics
8 minute read
Notice a tyop typo? Please submit an issue or open a PR.
Database Security Basics
Overview
Databases might contain sensitive information like medical records. We use access controls to manage this just like we would for files. The main difference with a database is that the data is structured, there is a schema that defines relationships within the database. There are still read/write permissions, but there instead of reading we make queries and instead of writing we have update transactions.
Again we deal with authentication and authorization, similar principles like RBAC apply here. A new issue is inference attacks, where multiple queries that are each individually allowed let the user infer sensitive data.
Example DB
The columns are (in order)
- Employee name
- ID
- Department
- Position
- Salary
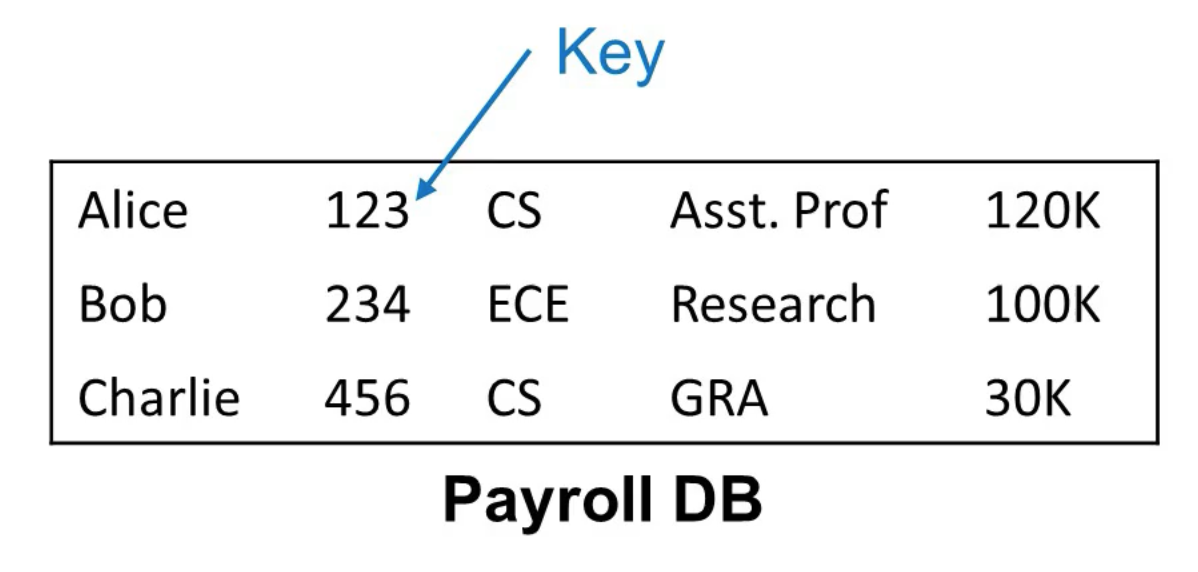
The ID is a special column known as a key.
With files we had read and write, tables have operations like select, insert, delete, update, and join. Permissions are given for these operations instead of just permission for read, write.
Here are some examples from the lectures -
GRANT "CREATE TABLE" to Manager [with admin option]
REVOKE "CREATE TABLE" from Manager
GRANT SELECT on TABLE to Manager [with Grant option]
REVOKE SELECT on TABLE from ManagerThese statements do things like allow/remove the ability to create tables and allow/remove the ability to run SELECT queries.
When we revoke it cascades, so if you revoke from someone who propogated the role, the people who got the role from the person you just revoked will also lose permissions. The last statement made will cascade in the above example.
admin vs. grant option
The admin option is like giving ownership access rights. They can revoke rights to someone who is granted rights. In this case rights that are granted will not cascade on revocation.
The grant option simply allows propogation and revocation to those who you granted to. If your permissions are revoked it will cascade.
Stored Procedures and Views
Stored procedures
Stored procedures are like applications that get run on the database. These applications need permission to perform operations on the underlying database.
Users can have permissions of either definer or invoker.
- Definer: The user can run the stored procedure without actually posessing the needed permissions to perform the various operations.
- Invoker: The user needs whatever permissions the procedure uses to operate on the underlying table.
Virtual Databases or Views
Views can be derived from tables within a database.
- You can access the view when you have permissions to access all the underlying tables of the view within the database.
- You can grant access to the view when you have grant permissions to all the underlying tables.
Inference attacks
Suppose we have public base salary and public total compensation in a database, but we want to keep the bonus private. This isn't possible since base salary + bonus = total compensation. This is an example of vulnerability to inference attack.
Functional Dependency Attack
This is when the value in column A determines the value in column B. So maybe rank determines salary.
Suppose we don't want to expose name and salary.
You could query for name and rank, then query for rank and salary, then you know name and salary.
Statistical Queries and Aggregate Results
Sometimes statistical or aggregate information is provided in a way that bypasses access control.
Consider that in school we like to know the distribution of grades, it is useful. But, we need to make sure we don't disclose any sensitive data.
Multiple statistical queries can in total provide information that discloses sensitive information.
Statistical Query Attack Example
The attacker has
- Some queries that return averages
- Some external information about things like the number of people in a certain demographic.
Suppose the attacker has the average GPA for male students, female students, and overall. If the attacker knows that there is only one female student in the class then we can say that
And then we solve for female, but since there is only one female student we know exactly who this is.
Defending Against Inference Attacks
Small/Large Query Attack and Mitigation
Here are some variables we need to define:
- N = total number of users in DB
- n = threshold set by system
- C = A characteristic like male or female. If female, then |C| is the number of female students.
So the mitigation is making sure we don't allow the query to include/exclude too small a group of people. We allow the query when:
Tracker Attack
We can defeat the mitigation. Suppose in the diagram below that C only contains 1 observation. We can query and (the shaded region), both of which are legal.
![]()
So now we can calculate stuff about C.
The Sad Truth
There is a theorem that says given an unlimited number of statistical queries that return correct answers, all statistical databases can be compromised.
Public Database
Maybe if we just remove personally identifiable information then we can publish all the data.
Here is a model of the situation where we set up a public database. The transformation step should preserve privacy while preserving usefulness of statistical queries.
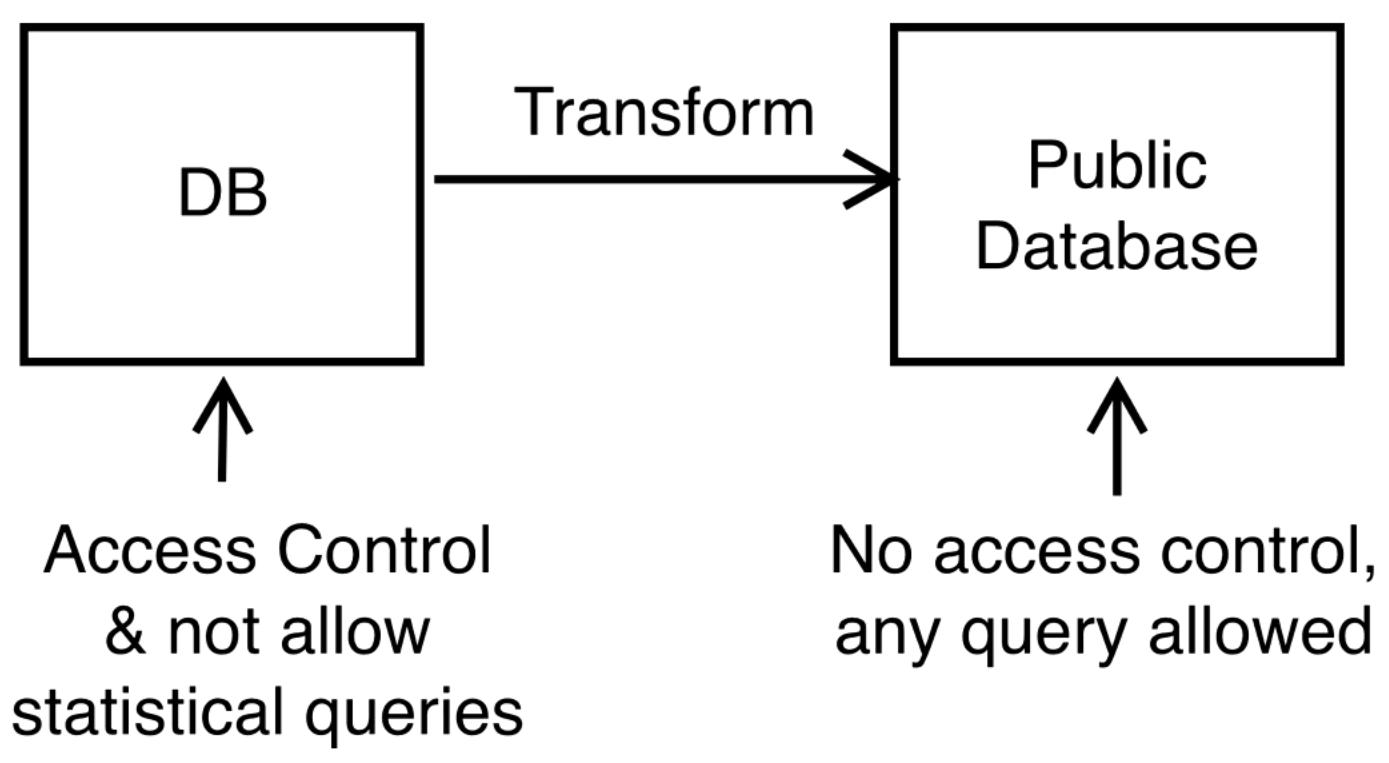
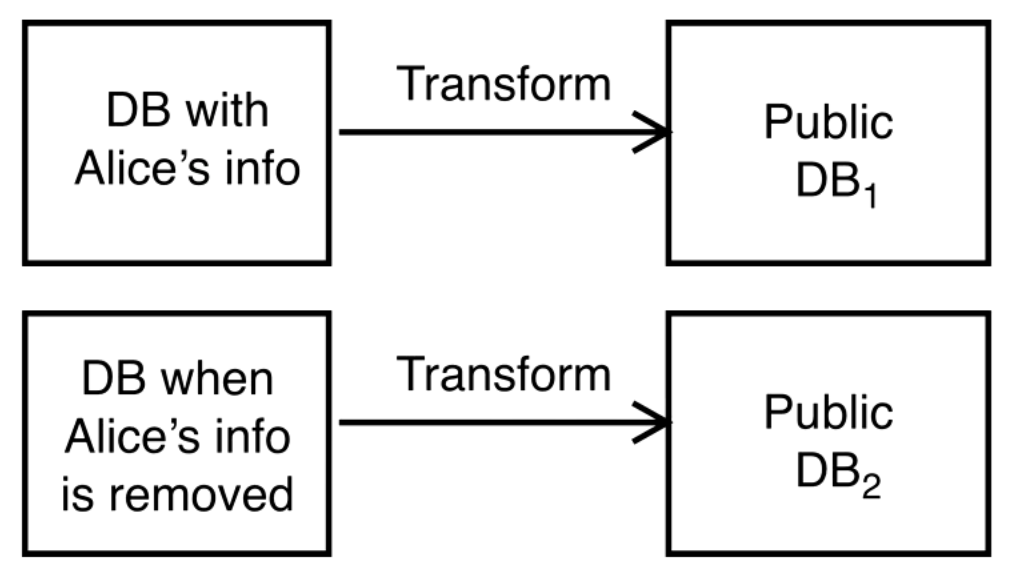
But what does it mean to preserve privacy? It means that whether someone's data is included or not that it makes no changes to their privacy.
De-identification
All identifying information from the users needs to be removed. This is things like
- Name, SS#
- Address cannot be included, maybe some more general data
- Date of birth maybe not, maybe the year is ok.
- No biometric data
- No pictures of the person
Two challenges are
- Can the de-identified information be linked to a person (linking attack)?
- Is the dataset still useful?
Here is an example where we removed the name. We don't want people being associated with medical conditions.
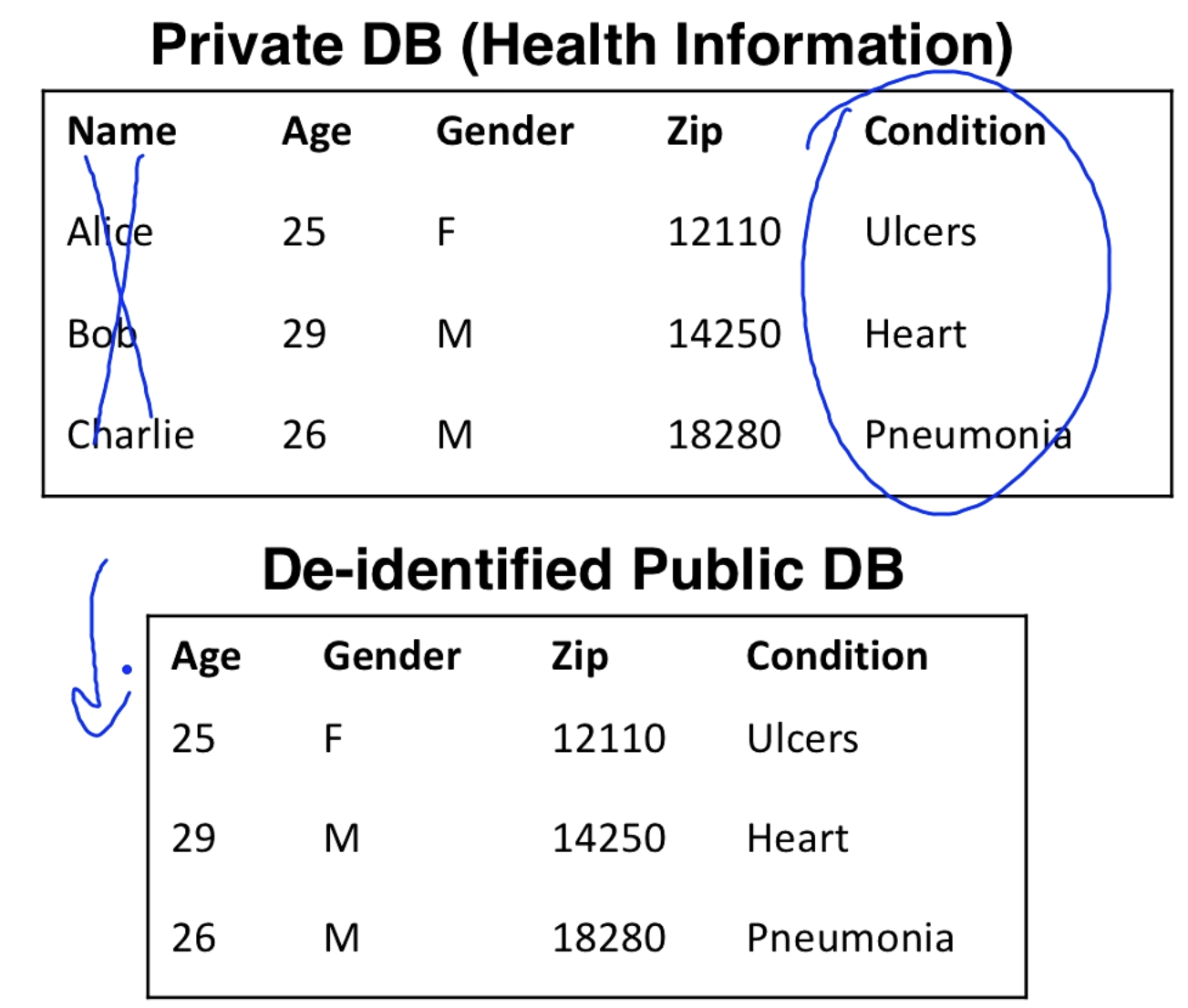
Attacks on De-identified DB
Some fields like age, gender, zip code can be used as a quasi-identifier (QID). QIDs can be combined with public information to figure out the identity of someone.
In one case the governor of Massachusets had a health condition found by the public using voter information.
We can make these attacks harder by replacing a specific value with a range of values (25-30 instead of 26).
Anonymization
K-Anonymity
K-anonymity means that at least k different rows have the same QID for any QID. In the example below the age and zip combination yields three different people.
This way it is much harder to link the QID to the condition.

Although we have increased the privacy we have decreased the utility, since researchers might like to know the exact age.
l-diversity
Even if there are 3 people for a certain QID it wouldn't help anonymity for the QID if they all had ulcers. If I can link a person to the QID I know exactly what condition they have.
l-diversity says that all rows of the same QID must have at least l distinct values in the sensitive data column.
We can increase diversity through increased generalization.
Differential Privacy
A user (potentially malicious) sends a query which submits the query, adds some noise, and returns the results.
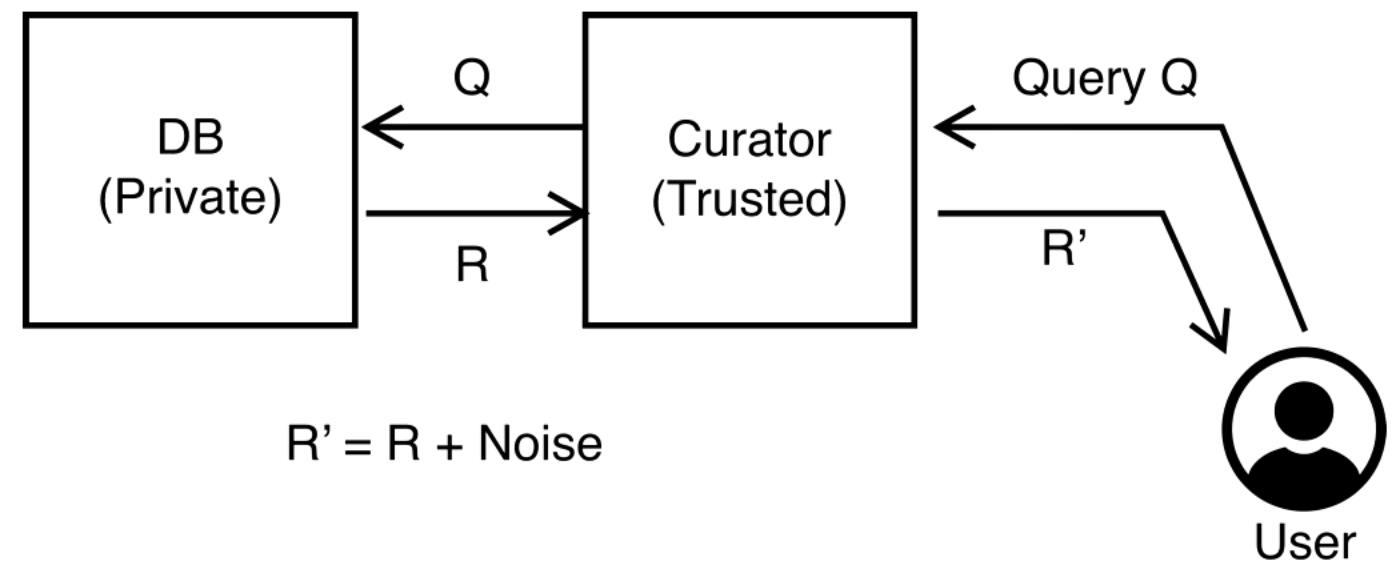
Some notation is introduced P[K(D) in S] which means that someone can determine a health condition for a person Alice. D is a database with Alice's data and D' is a database without Alice's data. The basic idea is that we shouldn't be able to distinguish between D and D' in terms of how useful they are to an attacker.
Some notation is introduced:
P[K(D) in S] is the probability of an attacker being able to figure out some information of interest about Alice with database D under a differential privacy scheme K. P[K(D') in S] is the probability of the attacker being able to figure out this thing if Alice's data is not in the database. With good differential privacy these numbers should be similar.
Our measure of privacy is , which is bounding the inequality -
Implementing Differential Privacy
We are trying to conduct a survey on how many people run red lights. We want people to be comfortable giving honest answers, so we need to provide them some privacy guarantees.
We set up a protocol where upon receiving a response R from the database we return R if we flip a coin and get tails and if we get heads then we flip the coin again and answer no if tails and yes if heads.
Analysis
- N is the total number of queries
- n is the number of queries returning yes
- p is the fraction of people who really break the law
The following formula basically says the people that run red lights (proportion p) are going to say yes 3/4 of the time, and the rest of the people say yes 1/4 of the time.
n = N*p*(3/4) + (1-p)*N*(1/4)
From this we calculate -
p = 2*(n/N) - 1/2
With enough queries we can estimate p.
We get plausible deniability for anybody that returns a positive response.
There is a sample calculation but I am not sure I understand where they are going with it. If you are able to speak confidently on this please submit a PR.
More Details
Differential privacy may use a Gaussian or Laplace mechanism to generate noise. There are some guarantees that can be made when using these distributions for noise.
Local differential privacy is when users locally perturb their data and share it, so there is no need for a trusted curator.
The main parameter in differential privacy is epsilon (). Small values are better, it is called the privacy budget.
Apple and Google claim to provide differential privacy. It is hard to make sense of this in the context of frequently collected data.
In the US census there is a law about protecting people's data.
OMSCS Notes is made with in NYC by Matt Schlenker.
Copyright © 2019-2023. All rights reserved.
privacy policy