Secure Computer Systems
Authentication
9 minute read
Notice a tyop typo? Please submit an issue or open a PR.
Authentication
Background
The OS/TCB/reference monitor has the property of complete mediation, meaning that whenever an application accesses physical memory it must pass through the TCB. The TCB decides if it should/should not grant access to resources. Authentication is how we determine who is making a request.
Logging In
The user must log in to prove their identity to the TCB. Once the user logs in they have a session, they don't log in for each request they make.
For authentication the user makes a claim about who they are, provides evidence for this claim, and the system verifies that the evidence is good. You could think of this in terms of usernames and passwords.
How do we know that we are actually talking to the trusted computing base, and not somebody else's trojan? There is something called the trusted path that makes sure we are actually talking to the TCB. For example, in Microsoft you could do ctrl+alt+del which would take you to the trusted path and no other place.
Authenticated users have a UID associated with their processes which provides the TCB with information about their identity.
Authentication Methods
Desired Properties
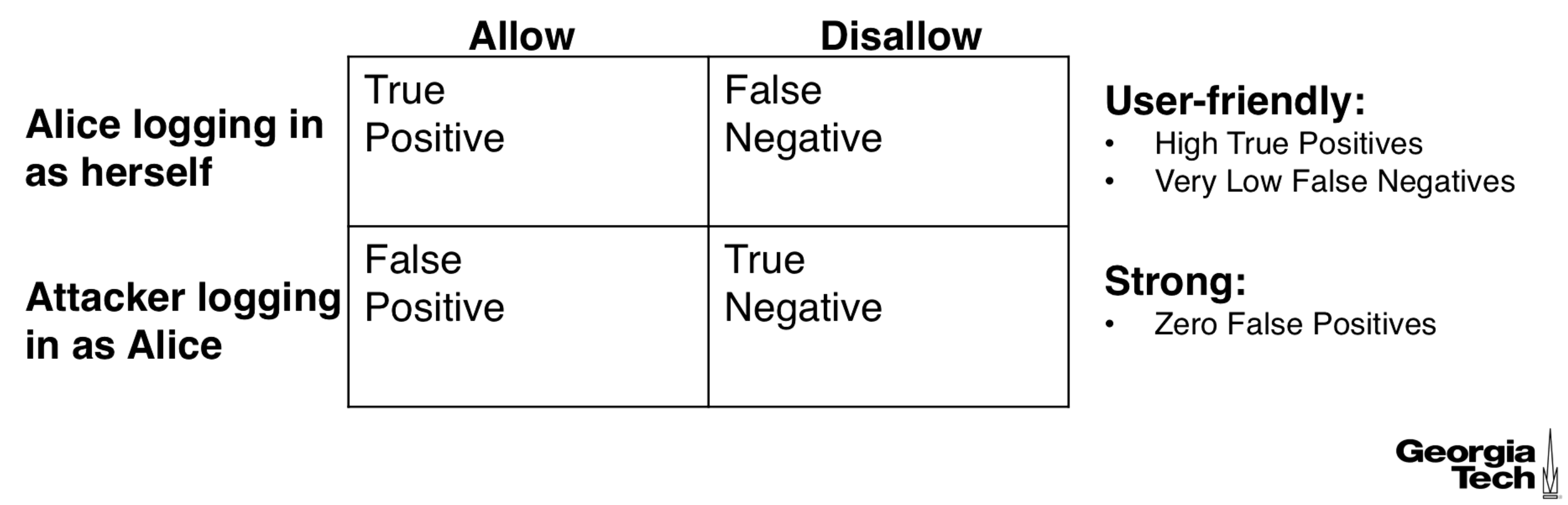
It should be easy for the correct user to log in (psychological acceptability), and it should be hard to break into someone's account (more work makes hacking less attractive economically).
The diagram below shows what a true positive, false positive, etc... are, along with some desired characteristics of our log in method.
How to Authenticate
The system should know some unique secret about the user. This secret can be -
- Something you know
- Something you have
- Something you are
The system will ask for this secret (password, a physical token, fingerprint) and authenticate you when it is provided.
Multiple authentication methods can be combined in multi-factor authentication. At GA Tech we do password (something you know) + cell phone (something you have).
Two Questions
- How is it implemented?
We usually assume the attacker can find the data stored if they break in. We store something other than the secret itself, like a hash with a salt. This way we can verify that a user has given the correct password without storing sensitive information.
Implementation details can be tricky for something like voice biometrics.
- How do we know how good the method is?
User acceptability says we shouldn't make life hard for the user. This means a high true positive rate.
We also want security, meaning 0 or very low false positives for an attacker of a given power. We can quantify something called guessing entropy to evaluate the strength of the system.
Guessing Entropy
Entropy
Entropy captures the expected amount of work the attacker must do to guess our secret. There is a formula:
Example: For an n-bit random secret the entropy is .
Question: What is the entropy for an 8 character password (upper case, lower case, digits, and special characters)
Answer: 26 lower, 26 upper, 10 digits, suppose we allow 6 special characters. This ends up being 68 character options. After simplifying our answer is . It is expected that you can perform this calculation.
Entropy and Work Factor
The work factor is the expected number of guesses the attacker needs to make. Learn about expected value calculations if you are not familiar.
, where
The guessing entropy is defined as
Example: Password Hardening
Password hardening is when the system uses both your password and your typing pattern to authenticate.
The two questions to ask are:
- How to implement it?
-
How good is it?
- From user acceptability standpoint
- From security standpoint
Implementing Password Hardening
The user has a username and a password. In addition to getting the password correct, we can make it so the user must type their password in a specific way, but how do we quantify the way that someone types?
For a password of length we measure
- How long a key is pressed
- How long it takes to move from one key to the next
There are key press lengths measured, there are transitions between keys, and so we are measuring time intervals.
These time intervals are characterized as fast, slow, or undefined. The undefined is for users that are neither fast nor slow. We say that being fast or slow is a distinguishing feature and that being undefined is a non-distinguishing feature.
These intervals are the feature vector. Password hardening requires that both the feature vector and the password match.
Instruction Table and its Entries
Passwords can be hashed and stored but our feature vector might vary across login requests due to non-distinguishing features. In this case we cannot simply hash and compare.
Our approach uses secret sharing. Secret sharing is when you split a secret into pieces and if you have a certain number of the pieces you can reconstruct the whole secret.
means that we split a secret into shares and need shares to reconstruct it.
We store these shares in an instruction table which is encrypted with the password. By typing at the right speed we are able to get of the shares from the secret sharing scheme. In the image below the value on the left is chosen when slow and the value on the right is chosen when fast. We choose total secret shares and all of them must be correct. If the true value is undefined the user can be either fast or slow. Below is a diagram of the instruction table.
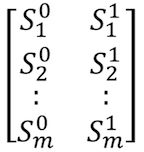
History File
The secret that we reconstruct with our secret sharing is the hardened password, which is used to encrypt the history file. The history file stores some number of past user login feature vectors. The history file is used to update the expected feature vector as the user's typing tendencies change.
password -> instruction table + feature vector -> hardened password -> decrypted history file
Upon successfully decrypting the history file we know the login was successful.
Upon Login
Every time you login the system changes the hardened password. Because the hardened password is our secret in the secret sharing scheme, this causes our secret shares to change. This way if the attacker compromises the instruction table it will just get changed on the next login.
After the user logs in we use this new data in the secret sharing scheme. Their login history's mean and standard deviation are used to categorize them as "fast" or "slow" on certain transitions and key presses. If the key press history is fast (mean + factor_standard dev < threshold), we put the correct secret share into the left side of the instruction table and garbage into the right side, if it is slow (mean - factor_standard dev > threshold) we put the good share on the right and garbage in the left. If neither, it is indistinguishing and we put good shares in both left and right of the instruction table.
Observations
The system requires nothing more than typing your password and no additional hardware (i.e. fingerprint scanner) is needed.
The hardening benefit is seen most when features are distinguishing and unique to users. If everybody is a fast typer there is no hardening benefit. We can make a tradeoff between hardening and usability by adjusting the size of our undefined typing speed region. The implementation updates to track drift in user typing habits via the history file.
Security Analysis
Suppose the attacker compromises the machine and has access to all of the information within.
- Trying to break into the history files requires the hardened password, which has high entropy.
- Finding the password requires guessing the password itself along with all the share combinations from the instruction table. This increases the work factor.
Suppose an attacker has installed malware to get the password. They still need to find the right feature vector.
This becomes a question of hardening entropy.
Hardening Entropy
Let's assume that each user has exactly 1 distinguishing feature and that the index of this distinguishing feature follows a uniform distribution.
On average it will take tries, which is . The hardening entropy is the logarithm of the work factor, so this is .
The lectures go into great detail on how to compute a lower bound for hardening entropy. Essentially, never guess undefined because it would have worked to guess fast or slow anyways.
The different feature vectors we need to try aren't just all possible feature vectors up to some length. We actually assume that the attacker has knowledge of the different possible feature vectors for all the different accounts. Giving the attacker this knowledge makes it a conservative estimate.
Then we calculate the expected value assuming that the attacker chooses their guesses with the highest probabilities first.
A formula is given, I really reccomend having a solid grasp on the lectures. But the amount of notation was a bit much and I thought it better to give my intuition.
An example is given where we calculate the hardening entropy for a special case using the derived formula, but it would be easier to just use the definition of entropy in this particular case because it is just picking out a password from random bitstrings of a given length, an example from the beginning of the module.
Something You Are - Biometrics
How do we implement it?
We need an interface to capture the user's biometric. We can compare this to a database of previously collected values. We can compare vectors to determine if the biometric is correct based on a threshold for acceptance or rejection.
Here is a diagram:
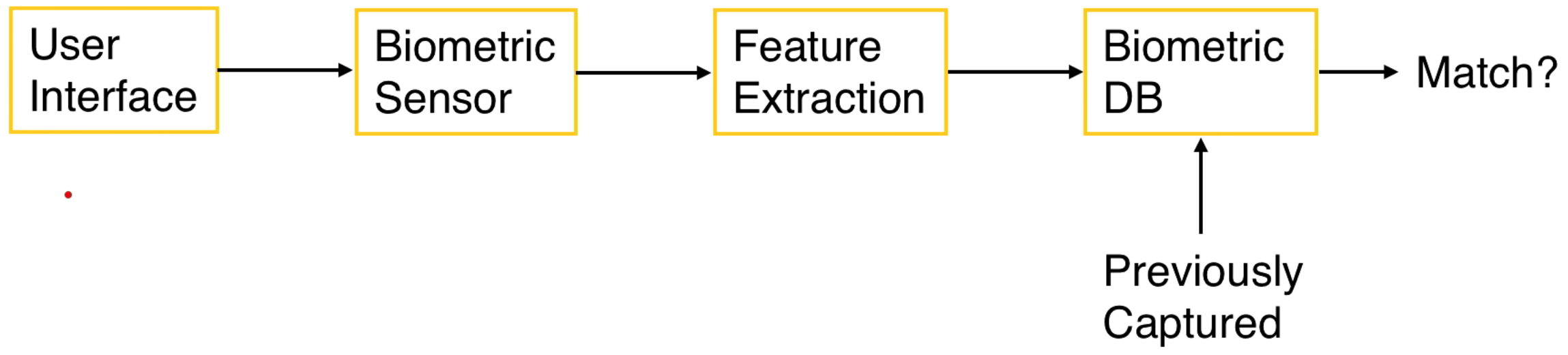
How do we evaluate it?
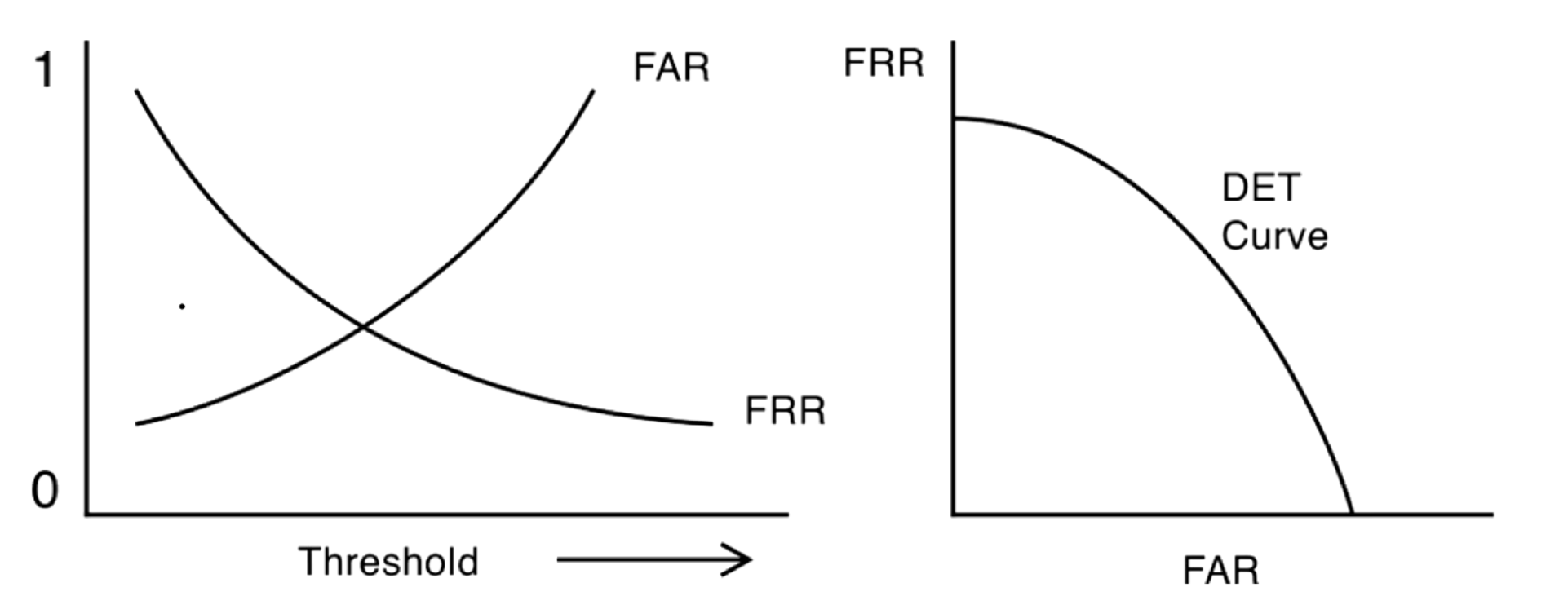
There is a False Reject Rate (FRR) and a False Accept Rate (FAR). There is a detection-error tradeoff (DET) curve. If we accept all input then FAR is 1 and FRR is 0. We want low FRR and low FAR, but there is a tradeoff. FRR effects usability and FAR effects security. One way to characterize the method is to calculate the equal error rate, the intersection of y=x and the DET curve.
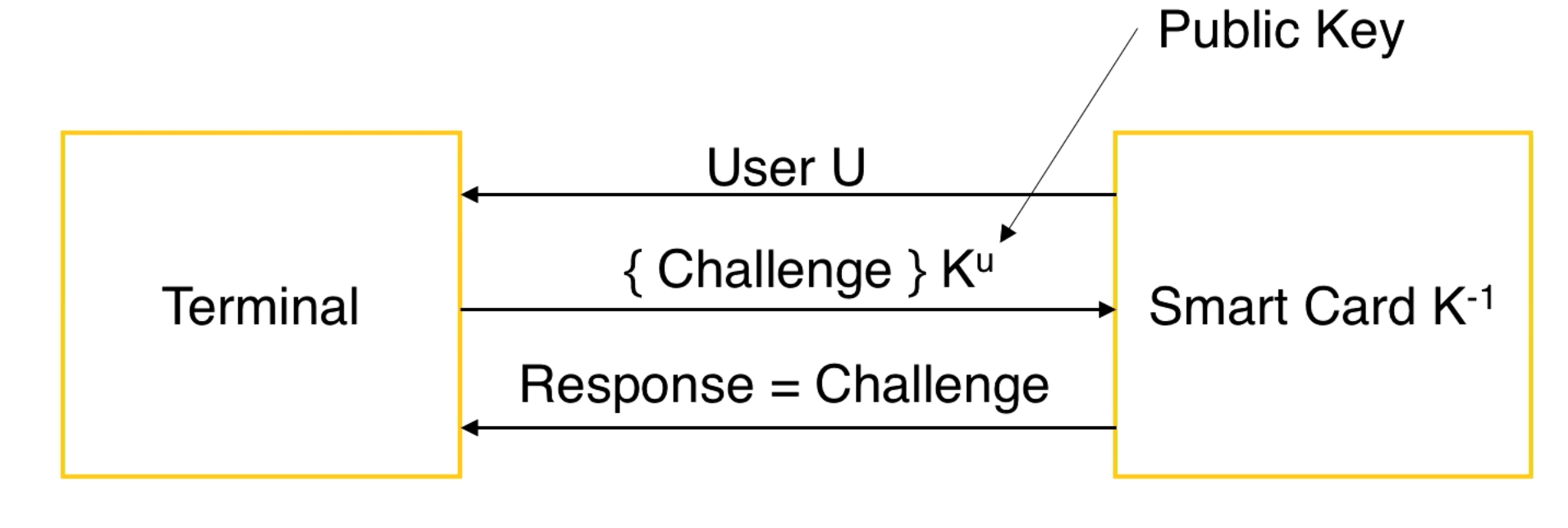
Other Methods: Something You Have and Know (Chip and PIN)
You put the card in the terminal, it gives you an encrypted challenge, you respond to the challenge by decrypting it with your private key and sending this decryption back to the terminal.
Attacks Against Authentication
Attacks might be against a weak authentication method or a weak implementation of an authentication method that isn't weak.
-
Stealing Passwords
- Poor choice of passwords (i.e. password123)
- Implementation errors (i.e. not hashing the password)
- Phishing attacks, key loggers, etc.
- Correct implementation is not easy.
- Implementation vulnerability found in chip and pin.
-
Biometric methods
- Have been attacks like taking fingerprint off of someone's glass.
OMSCS Notes is made with in NYC by Matt Schlenker.
Copyright © 2019-2023. All rights reserved.
privacy policy